Boundary Element Method

Fig. 1: Convergence history of the greedy reduced basis scheme for an acoustic duct problem. The intermediate relative residuals after the 1st, 6th and 9th iteration as well as the residual after convergence are shown. After the 6th iteration, we observe three maxima in the residual at the resonance frequencies of 100, 150 and 200Hz. These frequency points are subsequently chosen as sample frequencies for the computation of the basis vectors in iterations 7 to 9, leading to a fast convergence

Fig. 2: Illustration of boundary layer effects due to thermal and viscous losses. The arrows indicate the particle velocity in the propagation medium. The color scale provides information about the temperature variations in the fluid.

The boundary element method (BEM) is a popular numerical tool for solving linear time-harmonic acoustic problems arising in many technical and scientific applications. Using BEM, modeling is limited to the boundary of the wave-carrying fluid domain. While BEM is particularly advantageous due to the implicit satisfaction of the far field radiation condition, its major drawback stems from the frequency dependence of the coefficient matrices and the associated computational effort for frequency-wise response analyses.

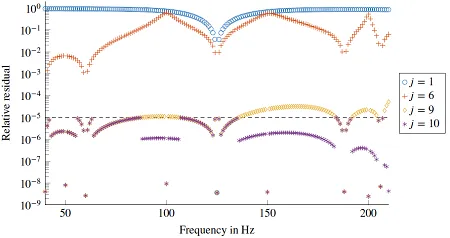
Therefore, at our chair, we develop numerically efficient strategies for obtaining frequency range solution with BEM. One of our recent contributions in this field is the so-called greedy reduced basis scheme. Given that the responses at a large number of frequency points are often contained in a small subspace, they can be well approximated by a few basis vectors. In our case, these basis vectors are simply solutions within the frequency range of interest that are chosen iteratively based on an optimality criterion.

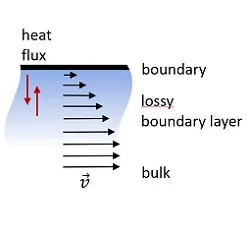
Further research projects focus on the incorporation of visco-thermal losses into the boundary element formulation. The latter are usually neglected when modeling sound waves because of their rather local character. Nevertheless, such small-scale effects play a crucial role in a large number of industrial applications. These include, for example, hearing aids or microphones whose cavities are of the same range as the lossy boundary layer. For the numerical description, our research team uses the so-called Kirchhoff dispersion law. In doing so, the linearized Navier-Stokes equations are decomposed into a viscous, thermal and acoustic mode, which only interact at the boundary. The implementation will enable advanced numerical studies of acoustic metamaterials.