Our research aims at development of efficient parallel methods in multiphysics and application to problems in science, engineering & medicine. Find an overview on our research topics below.
Digital Twin Model of the Cardiovascular System
The computational modeling of the cardiovascular mechanics represents a powerful tool for describing and understanding the heart function and diseases as well as predicting the effect of medical procedures.
The 3D-0D coupled closed-loop model of the heart and the vascular system delivers valuable quantities of interest for the physicians, such as blood pressure, blood flow and the contraction of the heart muscle. The heart muscle is modeled as a 3-dimensional nonlinear anisotropic elastic solid with an active material component, which simulates the cardiac contraction. The patient-specific geometry of the heart is extracted from medical imaging data such as computed tomography (CT) or magnetic image resonance (MRI) scans through a segmentation process. The entire vascular system is modeled with a reduced-dimensional lumped-parameter model, where each of the arterial and venous compartments of the systemic and the pulmonary circulation is described with a specific multi-element windkessel model.
A research project in collaboration with the German Heart Center Munich aims at building individualized Digital Twin models of adult patients with repaired tetralogy of Fallot (ToF) in order to predict the outcome of a pulmonary valve replacement. One of the most common late consequences after repair of ToF is pulmonary valve regurgitation. Significant pulmonary valve regurgitation progressively induces right ventricular dilation and dysfunction and increases consequently the risk of sudden death. While it has been shown that pulmonary valve replacement improves symptoms and functional status in these patients, the optimal timing and indications for the replacement intervention after repaired ToF are still debated. Therefore, a patient-specific Digital Twin supports the physicians in their decision-making by estimating the postoperative performance of the right ventricle. The cardiovascular Digital Twin is initially calibrated using preoperative catheter-based pressure measurements as well as MRI-based flow and geometry measurements.
- Hirschvogel, M., Bassilious, M., Jagschies, L., Wildhirt, S.M., Gee, M.W. (2017) A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics, Int. J. Num. Meth. Biomed. Engrg., 33, e2842. DOI.
Parameter Identification and Uncertainty Quantification in Personalized Cardiovascular Mechanics

One fundamental challenge in the computational modeling of personalized cardiovascular mechanics problems is the uncertainty that is ubiquitous in the patient-specific geometry, boundary conditions and material parameters of such models. If computational cardiovascular mechanics is to be used as a predictive simulation tool for diagnosis, research and decision making in clinical practice, robust and efficient uncertainty quantification (UQ) methods that deal with this lack of knowledge in a consistent manner are imperative. To that end, we advocate a probabilistic approach, where all available data obtained from measurements or via inverse analysis are specified in terms of probability distributions. We focus on the development and application of UQ methods that are feasible for large-scale problems and high-dimensional stochastic dimensions, in order to be able to infer information about the quantities of interest of the particular problem in the presence of uncertainty.
- Biehler, J., Gee, M.W., Wall, W.A. (2015): Towards Efficient Uncertainty Quantification in Complex and Large Scale Biomechanical Problems Using Approximate Models and Bayesian Formulations, Biomechanics and Modeling in Mechanobiology, 14, 489-513. DOI
- Biehler, J., Kehl, S., Gee, M.W., Schmies, F., Pelisek, J., Maier, A., Reeps, C., Eckstein, H.-H., Wall, W.A. (2017) Probabilistic noninvasive prediction of wall properties of abdominal aortic aneurysm using Bayesian regression, Biomechanics and Modeling in Mechanobiology, 16(1), 45-61, DOI.
- Bruder, L., Koutsourelakis, P.S. (2018): Beyond black-boxes in Bayesian inverse problems and model validation: applications in solid mechanics of elastography, International Journal for Uncertainty Quantification, 8(5), 447-482, DOI
- Bruder, L., Reutersberg, B., Bassilious, M., Schüttler, W., Eckstein, H.-H., Gee, M.W. (2019): Methoden der künstlichen Intelligenz in der vaskulären Medizin - Status quo und Ausblick am Beispiel des AAAs, Gefässchirurgie, 24, 539–547, DOI
- Bruder, L., Gee, M.W., Wildey, T. (2020): Data-consistent Solutions to Stochastic Inverse Problems using a Probabilistic Multi-fidelity Method Based on Conditional Densities, International Journal for Uncertainty Quantification, accepted
Lukas Bruder, Sebastian Kehl, Jonas Biehler
Peridynamics
Conventional methods such as the finite element method (FEM) for solid mechanics and fluid dynamics face natural restrictions at sharp edges and when cracks and very large deformations occur. Particle methods such as Peridynamics (PD) and related approaches are meshfree methods and do not have such limitations. One prime application is Additive Manufacturing (Selective Laser Melting), where a unified approach for thermodynamics, solid mechanics and crystal grain growth and transformation can be utilized.
Hybrid Preconditioning for Surface-Coupled Problems
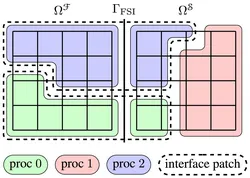
When solving coupled problems in a monolithic fashion, powerful preconditioning techniques are crucial to obtain an efficient solution scheme. In our group, we are interested in monolithic solvers for fluid-structure interaction problems, where a fluid and a solid domain exchange coupling information at their common coupling surface. Starting from well-established physics-based block preconditioners, that are known to accumulate the error at the coupling surface, we developed a novel hybrid preconditioner. It is based on an overlapping domain decomposition, that purposely exhibits subdomains that span across the fluid-structure interface. By performing cheap, but accurate subdomain solves in an Additive Schwarz manner in combination with the existing physics-based block preconditioners, the number of iterations of the linear solver as well as the total solution time could be reduced remarkably. Furthermore, scalability of the proposed methods has been demonstrated.
Parametric Model Order Reduction for Large Scale Problems
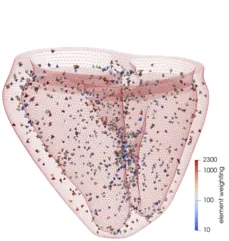
Model Order Reduction (MOR) is a technique under current research, which aims at a decrease of computational effort in large scale problems. The basic idea is to find a low dimensional subspace for the problem’s solution, while at the same time the quality of the solution shall be retained in comparison to a direct solution of the large scale problem. We aim at developing a MOR framework for finite element mechanical analysis of vascular mechanics problems. The reduction shall be performed for material as well as geometric parameters determining the mechanical properties as well as the geometry of the structure under consideration. The intended framework faces several complexities such as model nonlinearities, patient-specific geometries and hyper reduction.
Structural Topology Optimization
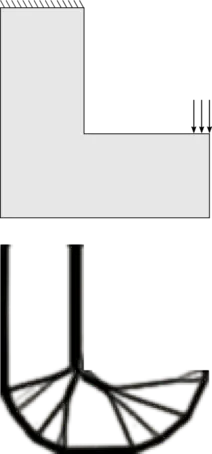
Topology optimization aims at the optimal distribution of material within a defined problem setting, that minimizes a given cost function and satisfies various constraints. Often the objectives are contradicting each other, such that a trade-off is required. A prime example is to create a structure that is stiff as well as light at the same time. Another optimization objective are the so-called compliant mechanisms. Those are structures that deform elastically to transfer energy from an input to an output port.
For three-dimensional problems, espacially considering geometrically non-linear mechanics, the designs obtained by an optimization algorithm are often against human-intuition. But the computer generated structures achieve better performance measures, than the classical designed counterparts.
The group focuses on efficient, parallel algorithms that enable the design of complex structures for general geometric non-linear structural problem formulations.
Design of Stents using Geometrically and Materially Nonlinear Topology Optimization
Chronic narrowing of the iliac arteries (IA) and/or femoral arteries (FA) due to atherosclerosis, is a common cause of the peripheral artery disease (PAD). PAD symptoms include restricted blood flow towards the lower limbs, which can lead to leg pain, skin ulcers, tissue death, and other severe complications. Atherosclerosis is commonly treated using angioplasty combined with stent placement. Unfortunately, interventions due to restenosis or stent failure are relatively frequent.
Stents within the IA/FA are especially prone to failure. In daily activities such as walking or sitting, the IA and FA undergo large deformations. This leads to bending, twisting and compression of the artery and the stent. The stent structure has to be flexible enough to follow these deformations, while exhibiting high radial forces to guarantee for sufficient blood flow. Current commercial stents are based on uniform patterns in terms of geometry and shape, which do not take into account large deformations. Commonly used superelastic nitinol stents exhibit excellent flexibility but lack required radial force properties. Therefore, a novel stent design, which allows for the necessary flexibility, but is radially strong, is desired.
We employ topology optimization (TO) to generate structures which satisfy the requirements of a stent within an IA/FA and additionally can be individualized to patient-specific geometries. TO is a established structural design method, able to generate non-intuitive designs for complex problem settings. The key idea is to achieve the flexibility by means of the geometric layout, rather than by material superelasticity and thus allow for non-superelastic material choices. To achieve this, the optimization model considers geometrically as well as materially nonlinear mechanics.
Functional Modeling of the Heart and an Extravascular Assist Device (VAD)

Due to decreasing number of transplantable hearts and deficiencies in current heart assist device technologies, novel concepts of extravascular heart assistance are developed in close collaboration between AdjuCor GmbH and MHPC. The collaboration aims at minimizing vulnerable impact to the heart and optimizing design and functionality of a novel device by use of computational models. Therefore, computational models of the heart, the vascular system and a novel epicardial augmentation device are developed and their interplay computed on patient-specific cardiovascular conditions in order to predict the increase in heart work required to maintain vascular perfusion. Furthermore, models of oxygen transport and ventricular disease progression after myocardial infarction should help to gain further insights into the specific device operating parameters required to sustain cardiac regeneration.
- Hirschvogel, M., Bassilious, M., Jagschies, L., Wildhirt, S.M., Gee, M.W. (2017) A monolithic 3D-0D coupled closed-loop model of the heart and the vascular system: Experiment-based parameter estimation for patient-specific cardiac mechanics, Int. J. Num. Meth. Biomed. Engrg., 33, e2842. DOI.
- Jagschies, L., Hirschvogel, M., Matallo, J., Maier, M., Mild, K., Brunner, H., Hinkel, R., Gee, M.W., Radermacher, P., Wildhirt, S.W., Hafner, S. (2017) Individualized Biventricular Epicardial Augmentation Technology in a Drug-Induced Porcine Failing Heart Model, J of American Society for Artificial Internal Organs (ASAIO), online ahead of print, DOI.
Multi Objective/Field Optimization of an Extravascular Assist Device (VAD)
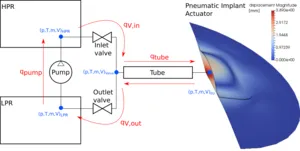
Faster rescue chains and especially improved clinical diagnostics and therapies have reduced the number of lethal heart infarcts. More patients survive but suffer from a resulting heart insufficiency. At the same time, heart transplantations are limited to the amount of donor organs, which has been declining during the past decade. A promising technology are efficient cardiac assist devices. However, the wide range of patient individual requirements makes it challenging to design an appropriate device. Together with AdjuCor GmbH, we develop a 0D model of the driving unit of a novel VAD and couple it to a 3D patient-specific heart model. This allows us to iteratively optimize device and implant in order to meet the individual patient needs.
A Multiscale Model of Atherosclerosis
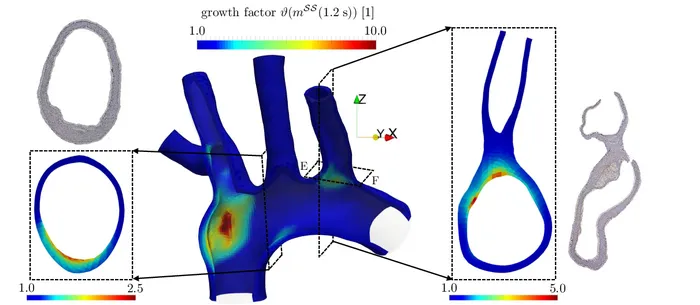
Atherosclerosis precipitates sequelae such as angina, heart attack and stroke, among others, and therefore is heavily involved in the leading causes of death in the western world. During atherosclerotic lesion formation, leukocytes, fatty substances, cholesterol crystals, cellular waste, calcium, platelets and fibrinogen accumulate in and on the intima and media of arteries, resulting in arterial wall thickening and subsequently continuous narrowing of the vessel lumen. Atherosclerotic plaque may rupture and expose its thrombogenic contents to the blood stream, leading to massive local blood coagulation and formation of a thrombus. Such thrombosis may lead to local and/or distal obstruction of blood vessels and gives rise to a major part of acute coronary deaths worldwide. The mechanical impact from blood flow and pressure imposed on the artery wall during atherosclerosis progression, its consequences on plaque composition and inflammation as well as the process of lesion formation with its interplay with biomechanical conditions, however, remain to be conclusively addressed.
In this project, a multiscale and multidisciplinary approach to the mechanobiology of atherosclerosis is taken that is based on computational techniques and experimental calibration and verification as well as in vivo molecular imaging. The biological processes involved take place at the (sub)cellular length scale and will be assessed experimentally by histology. Based on the imaged 3D geometries, macroscopic computational fluid-solid interaction models with transport and diffusion of species and cells supply an understanding of the local mechanical conditions which can then be correlated to the biological findings. A computational microscopic biological model will be implemented in a stochastic cellular potts model which will be coupled to the macroscopic continuum representation of the region of interest in a multiscale framework. Imaging of several stenoses in mice as well as carefully designed in vitro experiments are applied to test the hyphotheses of the model, calibrate its behavior and evaluate its predictive capabilities.
Moritz Thon, Almut Glinzer, Moritz Wildgruber, Alma Zernecke, Michael W. Gee, IGSSE
- Thon, M.P., Ford, H.Z., Gee, M.W., Myerscough, M.R. (2017) A Quantitative Model of Early Atherosclerotic Plaques Parameterized Using In Vitro Experiments, Bulletin of Mathematical Biology, online ahead of print, DOI.
- Thon, M.P., Hemmler, A., Glinzer, A., Mayr, M., Wildgruber, M., Zernecke-Madsen, A., Gee, M.W. (2017) A Multiphysics Approach for Modeling Early Atherosclerosis, Biomechanics and Modeling in Mechanobiology, online ahead of print, DOI.
- Glinzer, A., Xiaopeng, M., Prakash, J., Kimm, M., Lohöfer, F., Kosanke, K., Pelisek, J., Thon, M., Vorlova, S., Heinze, K., Eckstein, H.-H., Gee, M.W., Ntziachristos V., Zernecke, A., Wildgruber, M. (2017) Targeting elastase for molecular imaging of early atherosclerotic lesions, Ateriosclerosis, Thrombosis and Vascular Biology, 37, 525-533, DOI.
Coupling Methods and Time Integration in Fluid-Structure Interaction

Numerical analysis of fluid-structure interaction (FSI) phenomena plays an important role in many fields of applications like civil, mechanical, aerospace or biomechanical engineering. All these disciplines deal with highly dynamic problems, where a stable and accurate time integration is crucial in order to run useful simulations. The computational efficiency of the applied algorithms is of high interest, especially when it comes to real applications.
For some numerically very challenging FSI problems we could show that monolithic coupling schemes outperform partitioned approaches. The efficiency of the monolithic scheme is based on newly developed iterative solvers for the coupled linear system of equations.
We aim at developing time integration strategies for FSI problems with good stability, accuracy and efficiency properties. Implicit schemes seem to be appropriate for this type of problem. In order to gain more efficiency and reduce the computational costs, adaptive time stepping procedures are very promising, especially when large scale nonlinear problems are in the focus of interest.
Mayr, M., Klöppel, T., Wall, W.A., Gee, M.W. (2015): A Temporal Consistent Monolithic Approach to Fluid-Structure Interaction Enabling Single Field Predictors, SIAM Journal on Scientific Computing, 37(1): B30-B59, DOI.
Mayr M, Wall WA, Gee MW (2017): Adaptive time stepping for fluid-structure interaction solvers, Finite Elements in Analysis and Design, 141: 55-69, DOI: 10.1016/j.finel.2017.12.002
Analysis of Shape Variability of Abdominal Aortic Aneurysms
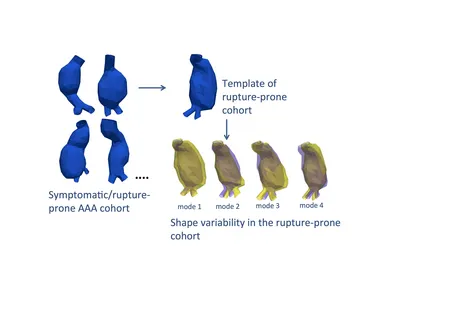
An abdominal aortic aneurysm (AAA) is a local dilation of the abdominal aorta, leading to shapes often threatened by rupture. In clinical practice, the classification between stable and rupture-prone AAAs is done according to one geometrical feature, i.e. the maximum diameter, a criterion that is well established, but proven to be not sufficiently accurate for rupture risk prediction. This project aims therefore at evaluating the rupture risk based on the whole patient-specific AAA abluminal surface. The groupwise statistics for the classification require the estimation of an averaged geometry, a template, of both the symptomatic/ known ruptured (rupture-prone) and asymptomatic AAA cohort found in the exemplary database. Then, each template is mapped to every AAA surface of both cohorts. The mapping properties are used for the classification and for understanding the shape variability of each cohort.
Numerical Simulation of Stent-Graft Deployment in Abdominal Aortic Aneurysm
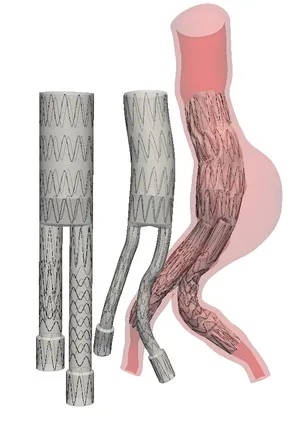
Endovascular aneurysm repair (EVAR) is a well-established technique to prevent rupture of abdominal aortic aneurysms (AAA). In this technology, a stent-graft (SG) is deployed inside the AAA to exclude the aneurysm sac from the main blood flow. However, EVAR involves some unfavorable complications such as endoleaks or SG migration. Such complications, resulting from wrong placement of the SG or incompatibility of SG design and AAA geometry, are difficult to predict. We aim at developing a predictive tool for the selection and sizing process of SGs depending on the patient-specific AAA geometry. A further objective of the predictive tool is a better risk assessment of the intervention indicating potential SG related complications already in the preoperative planning phase. The predictive, numerical tool based on finite element analysis requires the combination of various complex simulation components, such as contact mechanics between AAA and SG, mechanobiology of AAA, morphing strategies for the positioning of the SG and material modeling of the superelastic behavior of nitinol.
- Hemmler, A., Lutz, B., Reeps, C., Kalender, G., Gee, M.W. (2018): A methodology for in silico endovascular repair of abdominal aortic aneurysms, Biomechanics and Modeling in Mechanobiology, DOI
André Hemmler, Michael W. Gee, Christian Reeps, Brigitta Lutz, Günay Kalender
Block Multigrid Methods for Coupled Problems

Monolithic Formulations of Multiphysics Problems such as FSI lead to large sparse block systems of equations, where the coupling between individual fields expresses itself through respective off-diagonal matrix blocks. Iterative solution of these resulting linear systems of equations here is preconditioned by monolithic algebraic multigrid methods, where the multigrid hierarchy accounts for the underlying nature of the individual fields as well as the coupling off-diagonal blocks in the monolithis linear system.
Gee, M.W., Küttler, U., Wall, W.A. (2010): Truly Monolithic Algebraic Multigrid for Fluid-Structure Interaction, International Journal for Numerical Methods in Engineering, 85, 987-1016, DOI
Gee, M.W., Hu, J.J., Tuminaro, R.S. (2009): A New Smoothed Aggregation Multigrid Method for Anisotropic Problems, Numerical Linear Algebra With Applications, Vol. 16, pp. 19-37. DOI
Algebraic Multigrid for Convection Dominated Problems

In many fields of our research there is a desperate need for fast and efficient solvers. Multigrid Methods are among the best methods for solving symmetric positive definite systems. However, for many applications (CFD, Transport) convective phenomena play an important role and may dominate the whole process. Convective terms result in nonsymmetric linear systems that often turn out to be very challenging for iterative solving methods. We develop a new framework for algebraic multigrid preconditioners that is also appropriate for these kind of nonsymmetric systems. Furthermore it provides flexibility that allows the continued development of robust AMG solvers.
Inspired by Petrov-Galerkin smoothed aggregation methods we use different Galerkin projections for the prolongation and restriction operators. The key idea for our transfer operators is connected to approximating a Schur complement. With special Galerkin projections we preserve important low-frequency error components and limit the sparsity pattern of the multigrid transfer operators.
Wiesner, T., Tuminaro, R.S., Wall, W.A., Gee, M.W. (2014): Multigrid Transfers for Nonsymmetric Systems Based on Schur Complements and Galerkin Projections, Numerical Linear Algebra with Applications, 21, 415-438. DOI
Inverse Design Analysis and Prestressing of Structures
In simulation of biomechanical structures the patient specific geometry of the object of interest is very often reconstructed from in–vivo medical imaging such as CT scans. Such geometries therefore represent a deformed configuration stressed by typical in–vivo conditions. Commonly, such structures are considered stress–free in simulation. We therefore develop methods to introduce a physically meaningful stress/strain state to the obtained geometry for simulations in the finite strain regime and demonstrate the necessity of such prestressing techniques. One method is based on an inverse design analysis to calculate a stress–free reference configuration. The other method is based on a modified updated Lagrangian formulation.
- Gee, M.W., Förster, Ch., Wall, W.A. (2010): A computational strategy for prestressing patient--specific biomechanical problems under finite deformation, International Journal for Numerical Methods in Biomedical Engineering, 1, 52-72, DOI.
- Gee, M.W., Reeps, C., Eckstein, H.H., Wall, W.A. (2009): Prestressing in finite deformation abdominal aortic aneurysm simulation, Journal of Biomechanics, 42, 1732-1739 DOI.
Image Registration
Image registration plays a key role in a broad variety of clinical and industrial applications whenever information is encoded by images. Especially in clinical applications the acquisition of information is highly based on imaging techniques, such as computed tomography (CT), magnetic resonance tomography (MRT) or Ultrasound. E.g. the study and classification of processes such as growth & remodelling of arteries, the cardiac motion of the beating heart or the deformation of the lung during respiration highly rely on deformation information encoded by follow-up CT-scans or motion-MRT respectively.
However the bijective characteristic of a transformation, i.e. the unique and invertible mapping of material particles, is not captured by the above mentioned clinical imaging techniques. Thus image registration for deformation estimation constitutes an ill-posed inverse problem which is in need of regularization strategies. We focus on the application of “measurements” from image registration in material parameter estimation for finite element models.
Marina Bassilious, Sebastian Kehl
Inverse Analysis
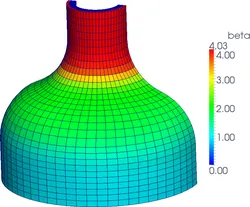
Material parameters for patient specific numerical models are subject to high inter-patient variability as well as to strong intra-patient spatial heterogeneity. Further it’s not possible to measure material parameters directly by means of non-invasive techniques. Thus accurate spatial representations of material parameters for the application in biomechanical models still pose a big challenge.
Inverse analysis methods provide a solution by trying to estimate material parameters according to a given reference solution, i.e. “measurements”. These measurements can be obtained non-invasively, e.g. by extracting deformation information from images using image registration techniques. Therefore these measurements are not only subject to noise but also subject to systematic sources of errors due to regularization in the image registration. Consequently the quality of the final estimation of material parameters highly depends on the quality of the measurements.
Our interest is on the development of efficient inverse methods to accurately estimate patient specific parameter distributions. Special focus is on methods to avoid the error propagation introduced by errors in the measurements.
Kehl, S., Gee, M.W. (2017) Calibration of parameters for cardiovascular models with application to arterial growth, Int. J. Num. Meth. Biomed. Engrg., 33, e2822, DOI.
Sebastian Kehl
Contact Mechanics and Mortar Methods
Mortar Methods
Domain decomposition techniques in general, and mortar methods in particular, provide very powerful tools for the numerical approximation and solution of partial differential equation (PDE) systems. Mortar methods are especially promising when geometrically non-conforming interfaces and / or non-matching triangulations are involved or when different discretization scheme must be coupled. Due to a manifold of reasons (e.g. different resolution requirements in different physical fields, complex geometries) this is most often the case in engineering practice.
Continuity conditions at the interfaces - usually enforced pointwise via collocation - are satisfied in a weak integral sense with mortar methods, which leads to a variationally consistent mixed formulation based on additional Lagrange multiplier degrees of freedom. The special focus of our research is on so-called dual Lagrange mutliplier spaces, which allow for a much easier realization of the coupling conditions by algebraic condensation of the interface terms. Notably, this approach does not impinge upon the optimality of the method in terms of spatial convergence.
Contact Mechanics
Our method development in the field of computational contact dynamics focuses on efficient finite element discretizations for fully nonlinear problems (finite deformations, nonlinear material behavior, friction) and non-matching meshes / non-conforming interfaces. Mortar methods, which originate from domain decomposition, have proven to serve as an ideal computational framework, as they allow for a variationally consistent treatment of contact interaction. Using so-called dual spaces for the Lagrange multiplier interpolation pairs the superior robustness of mortar methods with a significant increase of computational efficiency, while at the same time preserving optimal spatial convergence and other important properties of mortar methods. The simplification is mainly achieved by chosing dual shape functions based on a so-called biorthogonality condition, which avoid the necessity of solving a mass matrix system for the interface coupling problem.
The question of constraint enforcement is addressed with active set strategies interpreted as so-called semi-smooth Newton methods, which treat all nonlinearities (kinematics, material, contact, friction) within one single nonlinear iteration scheme. In contrast to the most commonly applied constraint enforcement techniques today, these methods do neither need an unphysical, user-defined parameter (e.g. penalty parameter) nor additional iterative schemes for the Lagrange multiplier update (e.g. Uzawa's method).
Finally, a special focus is also set on high performance computing and parallel scalability of the developed contact formulations, with efforts ranging from efficient search algorithms (including self contact) to dynamic load balancing strategies as well as state-of-the-art iterative solvers and preconditioners for contact problems.
High Performance Computing
A broad collection of methods and software in various aspects of HPC is developed at MHPC, among them:
- Baci - Multifield Code, mainly based on FE, joint with LnM
- ML, MueLu - Algebraic Multigrid Predconditioners
- Moertel - An abstract framwork for Mortar Mesh Tying
- Trilinos - Algorithms & Enabling Technologies at SNL
Besides, we regularly organize seminars and meetings (such as the EuroTUG) and of course teach important aspects of HP computing, e.g. in Advanced Parallel Computing & Solvers in Engineering
Finite Element Technology

Low order tetrahedral elements often are very convenient to use for discretization of highly complex geometrical shapes but also can suffer from poor mechanical behavior.
Here, we are interested in the development of low order elements based on nodal averaged strain quantities. Such element formulations provide very attractive mechanical properties but still remain extremely simple to implement and computationally efficient.
- Gee, M.W., Dohrmann, C.R., Key, S.W., Wall, W.A. (2009): A Uniform Nodal Strain Tetrahedron with Isochoric Stabilization, International Journal for Numerical Methods in Engineering, 78, 429--443, 2009. DOI.
Aortic Aneurysms and Cardiovascular Biomechanics

- Biehler, J., Gee, M.W., Wall, W.A. (2014): Towards Efficient Uncertainty Quantification in Complex and Large Scale Biomechanical Problems Using Approximate Models and Bayesian Formulations, Biomechanics and Modeling in Mechanobiology, published online. DOI
- Reeps, C., Kehl, S., Tanios, F., Biehler, J., Pelisek, J., Wall, W.A., Eckstein, HH., Gee, M.W. (2014): Biomechanics and Gene Expression in Abdominal Aortic Aneurysm, Journal of Vascular Surgery, 60, 1640-1647. DOI
- Reeps, C., Maier, A., Pelisek, J., Haertl, F., Grabher-Meier, V., Wall, W.A., Essler, M., Eckstein, H.-H., Gee, M.W. (2013): Measuring and Modeling Patient-Specific Distributions of Material Properties in Abdominal Aortic Aneurysm Wall, Biomechanics and Modeling in Mechanobiology, 12, 717-733. DOI
- Maier, A., Essler, M., Gee, M.W., Eckstein, H.-H., Wall, W.A., Reeps, C. (2012): Correlation of Biomechanics to Tissue Reaction in Aortic Aneurysm Assessed by Finite Elements and 18F-Fluordeoxyglucose-PET/CT, International Journal for Numerical Methods in Biomedical Engineering, 28, 456-471. DOI
- Marini, G., Maier, A., Reeps, C., Eckstein, H.-H., Wall, W.A., Gee, M.W. (2011): A continuum description of the damage process in the arterial wall of abdominal aortic aneurysms, International Journal for Numerical Methods in Biomedical Engineering, 28, 87-99. DOI
- Maier, A., Gee, M.W., Reeps, C., Pongratz, J., Eckstein, H.-H., Wall, W.A. (2010): A comparison of diameter, wall stress and rupture potential index for abdominal aortic aneurysm rupture risk prediction, Annals of Biomedical Engineering, 38, 3124-3134, DOI.
- Maier, A., Gee, M.W., Reeps, C., Eckstein, H.H., Wall, W.A. (2010): Impact of calcifications on patient--specific wall stress analyses of abdominal aortic aneurysms,Biomechanics and Modeling in Mechanobiology, 9, 511-521, DOI.
- Reeps, C., Gee, M.W., Maier, A., Gurdan, M., Wall, W.A., Eckstein, H.H. (2010): The impact of model assumptions on results of computational mechanics in abdominal aortic aneurysm, Journal of Vascular Surgery, 51, 679-688, DOI.
- Reeps, C., Gee, M.W., Maier, A., Pelisek, J., Gurdan, M., Wall, W.A., Mariss, J., Eckstein, H.H., Essler, M. (2009): The glucose metabolism in the vessel wall correlates with mechanical instability and inflammatory changes in a patient with a growing aneurysm of the abdominal aorta, Circulation: Cardiovascular Imaging, 2, 507-509, DOI.
Michael Gee, Sebastian Kehl, Jonas Biehler, Christian Reeps, Fadwa Tanios, Jaroslav Pelisek, Hans-Henning Eckstein
Experimental Biomechanics, Uniaxial/Biaxial Tensile Tests
For accurate numerical simulation of soft biological tissue or organs, as well as a deeper understanding of diseases, sophisticated material models are crucial. Soft biological tissue often exhibits nonlinear sometimes anisotropic properties and a complex fibre structure. In order to account for these properties in a computational model, by using an appropriate strain energy function (SEF), tensile tests are conducted and carefully evaluated. For anisotropic materials the information provided by uniaxial tensile tests is not sufficient to specify the form and the parameters of a strain energy function, thus biaxial tests are necessary.
Sebastian Kehl, Jonas Biehler