Melt Pool Modeling in Metal Additive Manufacturing
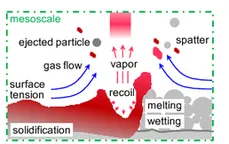
In the vicinity of the laser, powder particles begin to melt, leading to the formation of an - ideally continuous - melt pool. However, due to the complex melt pool and vapor dynamics arising from typical process conditions, melt pool instabilities may occur, entailing quality-degrading part defects such as evaporation-induced pores, spatter and lack of fusion. Understanding of the complex and competing physical phenomena governing the melt pool dynamics is mandatory to obtain a complete picture of defect formation, necessary to fully exploit the potential of powder bed fusion (PBF) additive manufacturing (AM) processes. The highly dynamic nature of the processes requires robust and efficient novel computational methods for capturing practically relevant length and time scales. By means of our SPH-based and FEM-based in-house melt pool modeling codes, we provide cutting-edge computational tools for explicitly resolving the detailed physics of the underlying physical processes in the melt pool, e.g., formation of the melt pool, mobile powder particles, interaction of the liquid and vapor metal phases as well as the inert gas.
Smoothed-particle-hydrodynamics-based Melt Pool Modeling
To gain a better understanding of the governing process physics and find optimal processing conditions for metal AM, a realistic model describing the melt pool dynamics is vital. Our ongoing research focuses on a modeling framework based on smoothed particle hydrodynamics (SPH) (Meier et al. 2021, Meier et al. 2021, Fuchs et al. 2022). The method's Lagrangian nature is beneficial in the context of dynamically changing interface topologies due to phase transitions and coupled microfluid-powder dynamics as present in the laser powder bed fusion (LPBF) process. The liquid and gas phase are described by the weakly compressible, instationary and anisothermal Navier-Stokes equations. Specifically, evaporation-induced recoil pressure (via a phenomenological model), temperature-dependent surface tension and wetting forces are considered. The solid phase consists of a substrate and mobile powder particles. Each mobile powder particle is modeled as arbitrarily-shaped mobile rigid body (three-dimensional continuum), allowing for contact interactions between powder particles, distributed temperature fields within the powder particles and continuous phase transitions.
The example below shows the melting process during LPBF of a substrate with 1500 powder particles. At the beginning, a stationary laser starts melting the powder particles and the substrate. Subsequently, the laser moves and creates a melt track. The melt front compresses the powder particles in front of the laser path, heavily distorting the powder bed. Additionally, recoil pressure forces eject (partially molten) powder particles from the melt pool.
Besides PBF AM, the generality and robustness of the computational framework also enables the modeling of other AM processes, like binder jetting or directed energy deposition.
Finite-element-based Melt Pool Modeling
Collaborators: Peter Munch and Martin Kronbichler both University of Augsburg
To describe mechanisms of defect creation, for example, creation of gas inclusions, accurately and to generally consider evaporation-induced gas/vapor flows and thereby induced material redistribution dynamics (e.g., powder particle entrainment by gas flow), a model is required with spatially resolved gas and vapor phase as well as liquid-vapor phase transition. Our ongoing research work focuses on the development of such a melt pool model by exploiting capalities of an Eulerian FEM-based framework. We model the extreme differences in material properties at phase boundaries (e.g. density ratio of molten metal to vapor ~1000-10000) by diffuse interface tracking schemes, such as level set or phase-field methods. This allows us to naturally capture a priori unknown moving interfaces and complex topology changes of the liquid metal-gas interface, such as keyholes, gas pockets, spattering, etc. To reduce the computational effort and in particular to allow for a high spatial resolution of the interface region, we consider adaptive meshing schemes. Further, to reduce the time for the matrix-vector product for solving the linear system of equations, highly efficient matrix-free solvers based on sum-factorization techniques for computing the integrals by quadrature are used. To this end, the implementation builds on top of the deal.II finite element library and the incompressible Navier-Stokes solver adaflo.
Below, on the example of the static laser melting of a bare metal plate, results from a numerical simulation of melt pool dynamics are shown. The high recoil pressure results in waves from the laser center to the edges of the melt pool and counteracting surface tension driven flow. The continuous laser energy input results in an increase in the amplitudes of flow oscillations and leads even to ejection of melt drops at the melt pool edges.
Publications
Please find publications on this topic here.