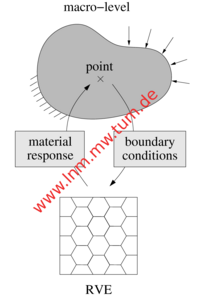
Our work focuses on so-called FE² methods which are based on a finite element discretization of both macro- and micro-level problems. Each macro-level integration point is implicitly identified with a representative volume element (RVE) representing the micro-structure in its vicinity. In each time and nonlinear iteration step, the macroscopic deformation state defines boundary conditions for the associated micro-problem. After solution of the nonlinear micro-problem, the macroscopic material response (i.e. stresses and constitutive tensors) is determined by volume-averaging over the RVE. The benefit of this strategy is twofold; firstly, an improved description of the macroscopic behavior is achieved. Secondly, phenomena on the micro-level can be investigated "on the fly".

One important field of application is lung tissue modeling. To enable a reasonable investigation of lung mechanics during (mechanical) ventilation, we developed a novel FE² approach for 3D nonlinear dynamics. This methodology is currently also utilized to deduce micro-scale material properties from macroscopic experiments in terms of a multiscale inverse analysis.