Discretization Methods: XFEM and CutFEM (eXtended and Cut Finite Element Methods)
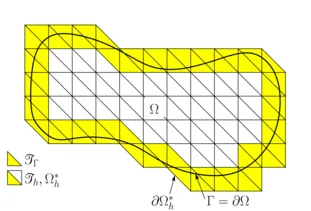
The extended finite element method (XFEM) was originally introduced for the simulation of cracks and other discontinuities in structures. As an extension to the classical finite element method (FEM), which uses continuous and continuous differentiable element shape functions, this numerical method enables the approximation of solutions involving sharp discontinuities like jumps and kinks within a finite element. Even non-homogeneous coupling conditions along moving complex shaped interfaces can be imposed. Despite of the time-dependent discontinuity location the need for mesh manipulation and remeshing can be avoided.
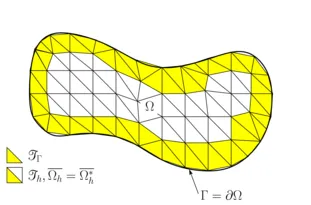
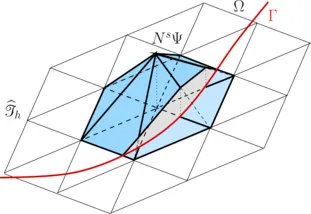
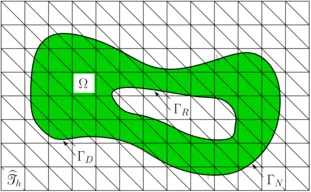
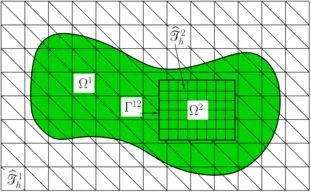
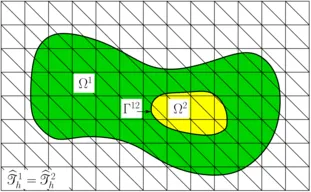
The representation of discontinuities requires additional degrees of freedom. Therefore, in the XFEM additional enriched shape functions are introduced. Their construction depends on the type of discontinuity and the interface location. The partition of unity concept is retained. For interface-coupled Multiphysics problems - equivalent to the use of jump enrichments in the XFEM - independent classical non-interface-fitted FEM approximations can be used for the participating phases. When they are cut-off at embedded boundaries or interfaces, the technique is designated as Cut Finite Element Method (CutFEM).
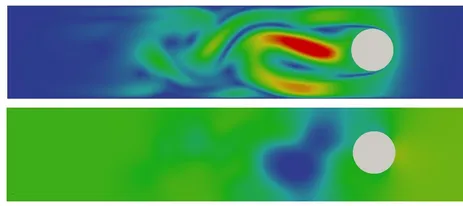
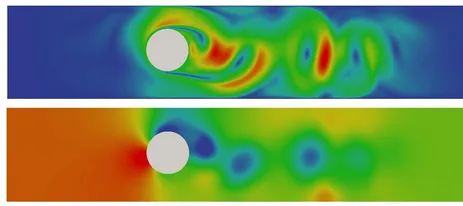
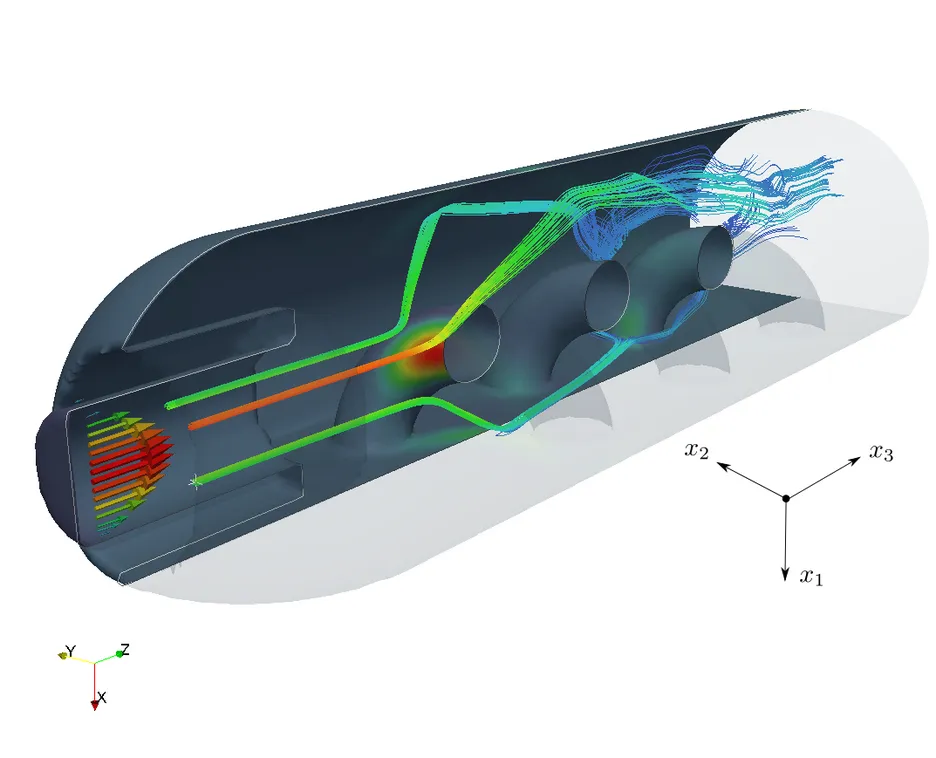
These techniques enable highly accurate novel discretization concepts applicable to, for instance, incompressible two-phase flow including surface tension, large deformation fluid-structure interaction problems, transport problems on largely changing topologies and future interface-coupled Multiphysics applications. Current research topics at our institute address contact of submersed bodies (fluid-structure-contact interaction), fluid-structure-fracture-interaction, fluid-poroelasticity-contact interaction, premixed combustion and the numerical simulation of biofilm structures.
As a result of the unfittedness of computational mesh and embedded boundaries, a substantial challenge for the XFEM and the CutFEM is the imposition of jump or other interior boundary conditions and constraints. These need to be enforced weakly. For this purpose we are developing powerful mixed-hybrid and Nitsche-type computational methods. Central focus in their development is turned to carry over numerical stability and optimal convergence properties from established boundary-fitted mesh configurations to the unfitted mesh case. All crucial approximation properties need to be guaranteed independent of the intersection location within the underlying computational grid. Moreover, in particular for transport problems, optimality needs to hold with respect to the different characteristic transport regimes. For this purpose, our research group focuses on the development of special stabilization techniques and drive their numerical analysis. As a further important prerequisite for the XFEM and CutFEM, we are developing a three-dimensional cut-library including efficient and accurate integration schemes.
Publications
Please find publications on this topic here.