Discretization Methods: Nitsche Methods
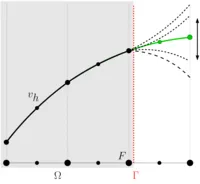
Nitsche’s technique provides a powerful computational tool for the weak enforcement of boundary conditions and interfacial constraints of partial differential equations in single- and multi-field problems. In contrast to Lagrange multiplier methods, which show severe restrictions with regards to the choice of pairs of approximation spaces for the primal field and the additional multiplier field to ensure an inf-sup stable scheme, Nitsche’s method uses a stabilization mechanism to guarantee optimality and stability. For this technique, no new multiplier variables are introduced into the system of equations. As a further important feature of this method for convective-dominated transport problems, in under-resolved boundary-layer regions constraints get automatically relaxed and thus provide more accurate, non-oscillatory results than simulations with strong enforcement strategies.
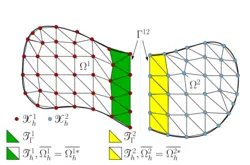
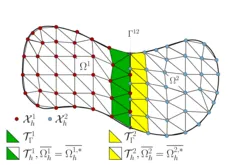
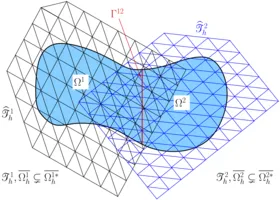
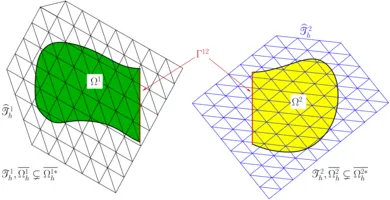
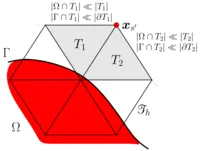
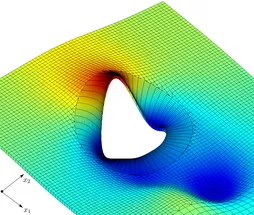
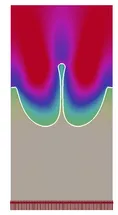
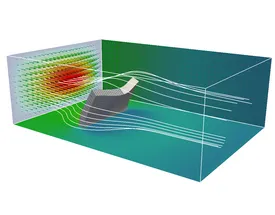
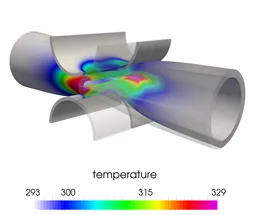
Over the past years, Nitsche’s technique found vast advancements towards domain decomposition and the weak imposition of essential and natural boundary conditions of Dirichlet-, Robin- and Neumann-type in fluid and scalar transport problems, and also in structural and contact mechanics. This class of methods is of particular importance when non-conforming or geometrically unfitted approximations are utilized, like in the XFEM and CutFEM. For such purposes, our institute developed stable and optimal convergent Nitsche-based schemes which in combination with so-called ghost-penalty stabilizations allow for the coupling of overlapping meshes in a geometrically unfitted fashion. The involved grids may consist of different mesh and material characteristics (e.g. different mesh sizes, aspect ratios, element types and shapes, polynomial orders, continuous and discontinuous Galerkin schemes, interface-fitted and non-fitted grids). This ability enables a great variety of novel discretization concepts which are highly relevant in engineering practice. Their applicability ranges from multiphase flow with high contrast in the material properties and large deformation fluid-structure interaction to fluid, solid and scalar field domain decomposition for complex shaped topologies or structural, thermo-mechanical and poroelastic contact mechanics.
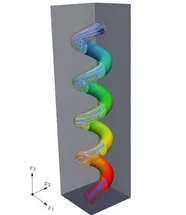
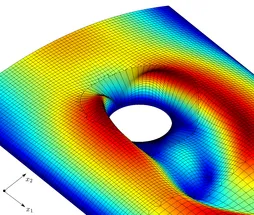
Applications of Nitsche-based techniques
Publications
Please find publications on this topic here.