psssMOR - Parametric Sparse State-Space and Model Order Reduction Toolbox
What is psssMOR?
psssMOR is a MATLAB toolbox for large-scale linear parametric systems in state-space. It provides functionality to define and analyze linear systems with parameter dependencies and includes algorithms for parametric model order reduction (pMOR) to obtain parameter-dependent reduced order models.
By defining large-scale parametric sparse state-space models with psss and subsequently reducing them with psssMOR, it is possible to drastically reduce the memory and computational requirements involved in the simulation, optimization and design of complex parameter-dependent dynamical systems.
The psssMOR toolbox is an extension of sss and sssMOR, and relies on the functionalities of these two toolboxes.
Large-scale linear parametric systems
The accurate modeling of dynamical systems often results in a large number of state variables and differential equations describing the system behavior over time. This is often the case, for instance, when discretizing partial differential equations in space over a fine grid or in the large-scale integration of electrical circuits.
In many real-life problems, the equations representing the system dynamics often depend on one or more design parameters. These parameters typically represent material properties, system geometry, operating points, boundary conditions, etc. Depending on the application, the parameter dependency might be analytically expressed or not, and may enter the models in a linear, affine or even nonlinear way.
Mathematically speaking, large-scale linear parametric systems can be modeled using state-space equations of the form:
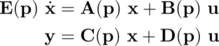
where the matrices depend on d parameters p = [p1, p2,..., pd]^T.
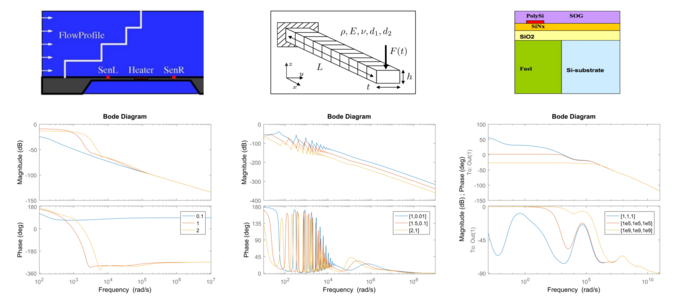
Naturally, parameter-dependent problems show different dynamics for various possible realizations of the underlying system. This fact is shown in the following figure for a selection of parametric benchmark problems (from left: anemometer (d=1), Timoshenko beam (d=2), microthruster unit (d=3)) evaluated at different parameter sample points:
Thus, large-scale linear parametric systems pose two big challenges for their analysis: first, the large state-space dimension complicates their numerical treatment and secondly, the parameter dependency leads to the need of repeated model simulation for many different values of the parameters.
To efficiently model and analyze high-dimensional linear parametric systems in MATLAB, we provide psss, which takes advantage of the sss toolbox, e.g. through the exploitation of the sparsity of large-scale systems.
Motivation for Parametric Model Order Reduction
Even when using psss functions to exploit the sparsity, performing multiple computations, such as simulations, on the expensive full order model (FOM) for different parameter values will require a substantial amount of time.
For this reason, we often seek a parameter-dependent reduced order model (ROM) of much smaller dimension that captures the relevant dynamics of the original model over a range of parameters. Hence, the goal of parametric model order reduction (pMOR) is to preserve the parameter dependency in the ROM, so that it is not required to repeat the whole reduction process for every new parameter value.
Similar as for linear non-parametric systems, parameterized linear systems are generally reduced by applying Petrov-Galerkin projections of the form:
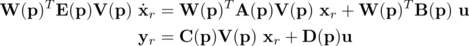
There exist several parametric model order reduction techniques to compute the parameterized reduced order model. One option is to compute global projection matrices V(p) and W(p) over the parameter space (usually generated from local projection matrices at multiple parameter values) and then use these global matrices to construct the parametric ROM. Another option is to compute local basis matrices V(pi) and W(pi) at different parameter sample points and then use these local matrices to construct the parametric ROM using different interpolation approaches (interpolation of local bases, of ROMs or of transfer functions).
psssMOR currently contains two pMOR methods: the Global Basis Approach (globalPMOR) as well as the Matrix Interpolation (matrInterp). For both algorithms, first a local reduction (localReduction) at different parameter sample points must be conducted to compute individual local basis matrices V(pi) and W(pi). The Global Basis Approach constructs then two global projection matrices from the projection matrices at the parameter sample points. These global matrices are then used for projection to reduce the system at new parameter points. In contrast to this, Matrix Interpolation applies first the local basis matrices for projection to construct local ROMs. These local reduced models are then interpolated during the online-phase to construct reduced order models at new parameter points.
Functionality of the toolbox
The toolbox mainly consists of two parts: the psss and the psssMOR modules.
psss functionality
psss allows to define, manipulate and analyze large-scale linear parameter-dependent systems by using parametric sparse state-space (psss) objects. The psss-class constitutes the crucial core of psss, since it allows to create psss-objects with user-defined parametric dependencies of the system matrices in a standarized way. Created psss-objects can be then manipulated, if desired, e.g. by fixing or unfixing certain parameters of the parametric system. In addition, non-parametric sparse state-space (sss) objects can be generated from a parametric system by specifying parameter sample points.
| Definition | Manipulation | Analysis | |
|---|---|---|---|
|
|
|
Furthermore, parametric systems can be analyzed for different parameter values using psss analysis functions such as bode, step, pzmap, etc. These functions strongly rely on the functionality of the same-named analysis functions of the sss toolbox.
psssMOR functionality
psssMOR includes algorithms for parametric model order reduction (pMOR) to obtain parameter-dependent reduced order models. Currently, the toolbox includes the Global Basis Approach as well as the Matrix Interpolation algorithm. Both algorithms can be decomposed into an offline and an online phase. During the offline-phase, reduced order bases and/or models are computed at user-defined parameter sample points using algorithms from the sssMOR toolbox (such as rk, tbr, irka, etc.). This local reduction is employed in localReduction. These local bases or models are then used during the online-phase to obtain reduced order models at new parameter points.
| Core functions | Global PMOR | Matrix Interpolation |
|---|---|---|
|
|
|
To learn more about the toolbox, you can...
- have a look at the psssMOR-slide for the talk "Automatic Adaptive Sampling in Parametric Model Order Reduction by Matrix Interpolation" presented at AIM 2017.
- download the toolbox and use the MATLAB doc to read our extensive documentation.
Download and set up the psssMOR Toolbox
Download v1.00, released 06 September 2017
| File | MATLAB version | Description |
| psssMOR Toolbox.zip | R2014b or newer | psssMOR + sss + sssMOR toolbox files (.mltbx), please run the "setup" file |
| psssMOR Toolbox (raw).zip | R2014a or older | psssMOR + sss + sssMOR raw files (.m), please run the "runme" file |
Getting Started
To open the documentation, type "doc" in the MATLAB Command Window. You will find it at the bottom right corner under Supplemental Software.
To open our demo, type "psssMOR_gettingStarted" in the Command Window.
Release Notes
psssMOR was developed in MATLAB 2016b. It has been tested for compatibility with MATLAB 2014b and 2015b both on Windows and Linux (Ubuntu 16.04.1 LTS). Previous MATLAB versions lack some of the capabilities exploited in sss, therefore its full functionality cannot be guaranteed for previous versions (though most functions may still work).
See also the MATLAB Central page for additional comments and information.
Newsletter
Sign up for our newsletter to stay up to date with new releases and publications.
Notes
psssMOR is free, open-source software distributed under BSD license to provide functions for large-scale linear parametric dynamical systems and foster the exchange of software and algorithms in academia.
psssMOR is developed in GitHub. The repository will be made public in the near future to allow for an easier exchange and common development of the functions. For comments, questions or submissions, please contact our team at morlab@...