Material Modeling: Computational Thermo-Plasticity
Alexander Seitz, Alexander Popp
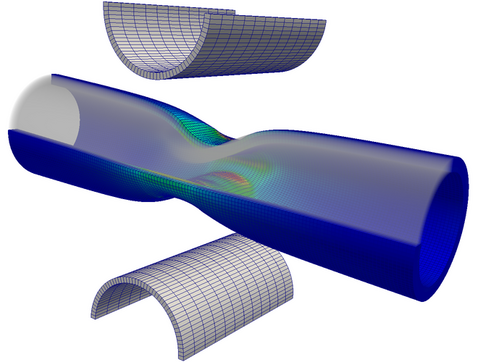
Plasticity plays an important role in many engineering applications from metal forming processes and structural failure to soil mechanics. The computational treatment of this nonlinear and even nonsmooth material behavior is usually done by the so-called radial return mapping algorithm. The plastic constraints are therefore enforced locally at each quadrature point. At finite strains, however, this well established method exhibits some weaknesses. For example, the efficiency of the radial return mapping usually relies on a specific choice of the hyperelastic constitutive law. Furthermore, it has a relatively small radius of convergence due to the strict enforcement of the constraints at each quadrature point and at each step in the nonlinear equilibrium iteration.
At our institute, a semi-smooth Newton method for computational plasticity is developed to tackle these issues. Therefore, the plastic inequality constraints are reformulated as a set of semi-smooth equations. The plastic flow at each quadrature point is introduced as additional primary variable and later eliminated from the global system of equations via static condensation. By introducing these additional degrees of freedom, convergence to the correct solution is achieved without having to enforce the constraints at each step in the nonlinear equilibrium iteration. Consequently, this approach results in a more robust algorithm.
Our algorithm incorporates general hyperelastic material laws, isotropic and kinematic hardening as well as plastic anisotropy. For the application to rocket nozzles, this algorithm is extended to thermo-plastic effects, including thermo-elasticity, temperature dependent material properties and heating due to plastic energy dissipation. The fully coupled thermo-mechanical problem is then solved simultaneously using efficient block preconditioners.
Finally, a uniform treatment of thermo-plasticity along with other nonsmooth effects such as frictional thermo-mechanical contact is obtained by the use of a semi-smooth Newton method. All nonlinearities including the active set search for plasticity and contact are then treated within one single nonlinear equilibrium iteration loop.